Efficient Huffman Decoding
Oct. 29, 2011
A while back, I posted an article examining the details of the GZIP compression algorithm. GZIP depends, among other things, on Huffman code compression. If you're not familiar with Huffman coding, take a look at my earlier article - I tried to explain the concept in pretty minute detail. In general, though, the idea behind Huffman coding is to use variable length codes to efficiently represent data. The 8-bit ASCII code, for example, is unambiguous, but inefficient — common characters, like the space code 0x20, take up the same amount of space in the input file as less common characters like the letter Q (0x51). The Huffman code assigns short codes to common characters and longer codes to less-frequently-occuring characters. Doing this correctly is somewhat tricky, since the inflater must be able to unambiguously decode the deflated result. As such, Huffman codes require that no two codes share a common "prefix" - if a 0011 is a code, then no other code can start with 0011. This is the prefix property that makes Huffman coding work correctly.
However, beyond the concept is the actual implementation. Although the easiest to understand (IMHO) implementation of Huffman codes and Huffman code inflation is tree-based, as detailed in my previous article, it's not, as wolf550e over on reddit points out, very fast, nor is it very memory efficient. In fact, the implementation I presented in my previous article uses two pointers for every bit in the Huffman table. This adds up pretty quickly, in terms of both memory usage and decoding time. A better implementation is the table-based one that the open-souce gzip application uses.
To see how this works, imagine a Huffman tree that encodes four symbols: A, B, C and D. A simple Huffman coding for these four symbols might be 0, 10, 110, 111. Now, the string ABCD would be encoded as 010110111, and the string DCBA would be encoded as 111110100. The trick to making this memory efficient is to store the codes left-aligned in a byte; then each code can be compared, masked off, to the current byte to find the symbol that it represents. Once a match is found — and remember, the Huffman coding ensures that the match will be unique — the symbol is output, the input is left-shifted, and another comparision is made. So, for example,
typedef struct
{
unsigned char code;
unsigned char mask;
unsigned int symbol;
}
huffman_code;
Listing 1: a Huffman tree structure
The Huffman code described above would be loaded into memory as:
huffman_code codes[ 4 ]; codes[ 0 ].code = 0x0 << 7; // binary 00000000 codes[ 0 ].mask = 0x80; // binary 10000000 codes[ 0 ].symbol = 'A'; codes[ 1 ].code = 0x02 << 6; // binary 10000000 codes[ 1 ].mask = 0xB0; // binary 11000000 codes[ 1 ].symbol = 'B'; codes[ 2 ].code = 0x06 << 5; // binary 11000000 codes[ 2 ].mask = 0xE0; // binary 11100000 codes[ 2 ].symbol = 'C'; codes[ 3 ].code = 0x07 << 5; // binary 11100000 codes[ 3 ].mask = 0xE0; // binary 11100000 codes[ 3 ].symbol = 'D';
Listing 2: a Huffman coding
Now, to decode the sample string 010110111, you compare:
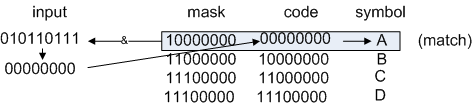
Figure 1: Looking up the symbol "A"
left shift by 1, get 10110111.
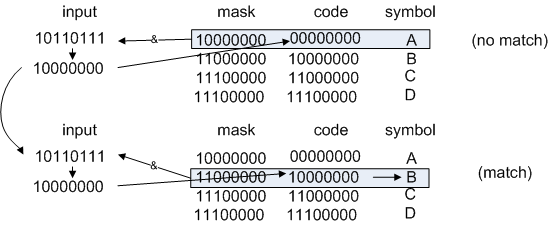
Figure 1: Looking up the symbol "B"
left shift by 2, get 110111
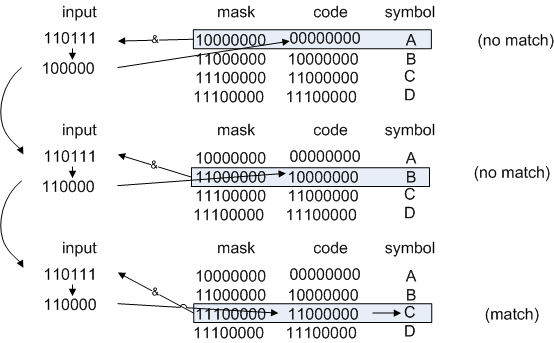
Figure 1: Looking up the symbol "C"
and so on. This works, and is about as memory-efficient as you could ask for.
You don't get something for nothing, though - this representation is not very time efficient. Every single huffman code requires a linear search of the code table. Since gzip typically produces several Huffman tables, some of which are on the order of 300 symbols, this is a pretty big performance hit.
So what can be done to speed this up without sacrificing memory efficiency? Well, the key observation is that each code in listing 2 is a number between 0 and 7 - if you don't mind using a little extra memory, you can use these as the indices into the table itself! This means that the table is, at a minimum, 8 entries — but this is still a major memory savings over the table-entry-per-bit approach outlined in my previous article.
codes[ 000 ].mask = 0x80; codes[ 000 ].symbol = 'A'; codes[ 100 ].mask = 0xB0; codes[ 100 ].symbol = 'B'; codes[ 110 ].mask = 0xE0; codes[ 110 ].symbol = 'C'; codes[ 111 ].mask = 0xE0; codes[ 111 ].symbol = 'D';
Listing 3: An index-based Huffman tree structure
But wait - if the code is the index into the table; which index do you look up? After all, all you have is the compressed input 010110111. How do you know what to mask it off by to do the table lookup? The key is the prefix property. Look at the table entries:
| code | mask | symbol |
|---|---|---|
| 000 | 100 | A |
| 001 | unused | unused |
| 010 | unused | unused |
| 011 | unused | unused |
| 100 | 110 | B |
| 101 | unused | unused |
| 110 | 111 | C |
| 111 | 111 | D |
Table 1: Index-based Huffman code table
Notice that the code for 'A' is 0 - and every entry in the table whose index starts with 0 is either the entry for 'A', or it's unused. This isn't a conincidence — this is part of what makes the code a valid Huffman code in the first place. In fact, my decision above to assign the ordinal 0 to the code "A" was techincally invalid - the code for "A" is just a binary "0" by itself. So instead, you fill out the table this way:| code | mask | symbol |
|---|---|---|
| 000 | 100 | A |
| 001 | 100 | A |
| 010 | 100 | A |
| 011 | 100 | A |
| 100 | 110 | B |
| 101 | 110 | B |
| 110 | 111 | C |
| 111 | 111 | D |
Table 2: Fully populated index-based Huffman code table
Now, to decode the input, just grab the next three bits from the input, look them up in the table, and put back the bits that weren't used (you have to consult the "mask" property to figure out how many you didn't use; it's still important here). So, to parse the sample input from above:Input = 010 110111 codes[ 010 ].symbol = "A", output "A" codes[ 010 ].mask = 100, so put back 2 bits Input = 101 10111 codes[ 101 ].symbol = "B", output "B" codes[ 101 ].mask = 110, so put back 1 bit Input = 110 111 codes[ 110 ].symbol = "C", output "C" codes[ 110 ].mask = 111, so don't put back any bits Input = 111 codes[ 111 ].symbol = "D", output "D" codes[ 111 ].mask = 111, so don't put back any bits
Example 1: Decoding using the index-based Huffman table
In fact, with this implementation, it doesn't make sense to store a "mask" anymore - all you really need to store is the number of bits to put back after the lookup is complete.So now the lookup is fast, and the memory requirements seem modest — the lookup table contains 2bits entries, where bits is the length of the longest code. This doesn't sound too bad, until you consider that in real implementations, the Huffman codes can grow to 12 or more bits. Such a table in this implementation would grow to 4,096 entries — to store at most a few hundred codes.
The tradeoff employed by gzip is to use a "multi-level" table. The first n bits encode the smallest entries directly — longer codes contain pointers to other tables. The key observation here is that the longer codes occur less frequently in the input (that's why they were assigned longer codes to begin with, after all), so it's worth the performance tradeoff if it takes a little bit more time to look up the longer codes, as long as the shorter code can be looked up quickly.
To see how this is implemented in practice, consider the longer Huffman code table below:
0000: 257 0001: 258 0010: 259 00110: 32 00111: 101 01000: 260 01001: 261 01010: 262 01011: 263 01100: 265 01101: 266 01110: 267 011110: 49 011111: 97 100000: 99 100001: 100 100010: 105 100011: 108 100100: 110 100101: 111 100110: 114 100111: 115 101000: 116 101001: 264 101010: 268 101011: 269 1011000: 10 1011001: 40 1011010: 44 1011011: 45 1011100: 46 1011101: 48 1011110: 50 1011111: 51 1100000: 53 1100001: 54 1100010: 56 1100011: 59 1100100: 61 1100101: 95 1100110: 98 1100111: 102 1101000: 104 1101001: 109 1101010: 112 1101011: 117 1101100: 270 1101101: 271 1101110: 272 11011110: 34 11011111: 38 11100000: 41 11100001: 42 11100010: 43 11100011: 52 11100100: 55 11100101: 57 11100110: 60 11100111: 62 11101000: 69 11101001: 103 11101010: 106 11101011: 118 11101100: 119 11101101: 121 11101110: 125 11101111: 273 11110000: 274 11110001: 275 111100100: 33 111100101: 37 111100110: 39 111100111: 47 111101000: 58 111101001: 65 111101010: 67 111101011: 68 111101100: 70 111101101: 73 111101110: 77 111101111: 78 111110000: 79 111110001: 82 111110010: 83 111110011: 84 111110100: 85 111110101: 91 111110110: 93 111110111: 107 111111000: 120 1111110010: 35 1111110011: 63 1111110100: 66 1111110101: 72 1111110110: 76 1111110111: 88 1111111000: 122 1111111001: 123 1111111010: 124 1111111011: 276 1111111100: 277 1111111101: 279 11111111100: 80 11111111101: 90 11111111110: 92 11111111111: 256
Example 2: A real-world Huffman code
This is the literals/lengths Huffman tree from the example in my previous article. This table encodes 105 symbols, ranging in lengths from 4 to 11 bits. Representing this using the lookup approach detailed above would result in a 2,048 entry table, 1,943 of whose entries would be redundant. Notice, however, that the bulk of the table (the first 89 entries) are 9 bits or less. Somewhat arbitrarily, gzip chooses to create a 9-bit table — exactly as detailed above — to encode these first 89 entries. This is a 29=512-entry table, saving quite a bit of memory over the naive 211-entry possibility.This does mean, however, that the remaining 16 entries require special handling. The gzip approach is to introduce a special marker on these "too long" entries that tells the inflating code that the entry is a pointer to another lookup table. Looking at the last 16 entries, you can see that this means that there will be 7 such multi-level entries in the resulting Huffman code table.
111111001 0: 35 111111001 1: 63 111111010 0: 66 111111010 1: 72 111111011 0: 76 111111011 1: 88 111111100 0: 122 111111100 1: 123 111111101 0: 124 111111101 1: 276 111111110 0: 277 111111110 1: 279 111111111 00: 80 111111111 01: 90 111111111 10: 92 111111111 11: 256
Example 3: Second-level Huffman code tables
To see this in action, consider decoding the input sequence:
100010100100111111001011111111110First, grab 9 bits of the input and index into the first-level lookup table:
table[ 100010100 ].code = 105, output 105 table[ 100010100 ].length = 6, put back 3 bits Input is now: 100100111111001011111111110Remember that the table itself has 512 entries, and every entry whose first 6 bits are 100010 are duplicates of one another.
Grab 9 more bits, index again:
table[ 100100111 ].code = 110, output 110 table[ 100100111 ].length = 6, put back 3 bits Input is now: 111111001011111111110Selecting the next 9 bits, we see that the table entry include a special "pointer" code:
table[ 111111001 ].ptr = table2Since this was a secondary table, the code knows that all 9 bits were used up, so none need to be put back. The input is now:
011111111110table2 is a 1-bit table; this means that the index is a single bit.
table2[ 0 ].code = 35, output 35 table2[ 0 ].length = 1, no need to put back any bitsThe input is now:
11111111110Looking up the next 9 bits in the table, we find that table[ 111111111 ] is a pointer to another table; in this case, the table is a 2-bit table (call it table3):
| index | code | length |
|---|---|---|
| 00 | 80 | 2 |
| 01 | 90 | 2 |
| 10 | 92 | 2 |
| 11 | 256 | 2 |
Table 3: A four-entry second-level Huffman table
So, grabbing the final two bits of input, we see that:table3[ 10 ].code = 92, output 92 table3[ 10 ].length = 2And the input has correctly been decoded as the sequence: 105 110 35 92.
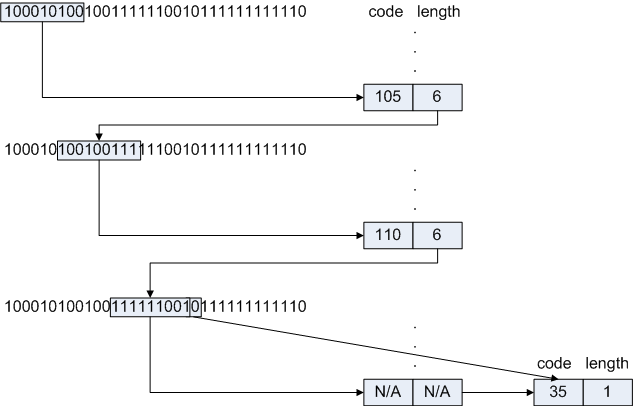
Figure 4: Efficient Multi-level table lookup
This scheme allows for arbitrary levels of table nesting, but I can't imagine (nor have I ever come across) a case that would require more than a single level of nesting.
So - why 9 bits in the table above? Why not 8? Or 10? Well, an 8-bit table would have had 256 primary table entries, but 37 of those entries would be pointers to second level tables, slowing down the inflation process a bit. A 10 bit table would have been faster at inflation time, since there would only be one extra table, but the primary table would have been twice as large, at 1,024 entries.
In the case of the literal/length table in the gzip compression algorithm, the table encodes a maximum of 286 codes (255 literal codes, one stop code, and 30 "back pointer" codes). Note that this is specific to the usage and has nothing to do with Huffman codes in general. A flat, non-Huffman-encoded table with 286 entries would need about log2 286 ≈ 8.16 bits to encode. Rounding up, you get 9 bits, which is the optimal speed/space tradeoff for the Huffman table. In fact, this value is hard coded into Mark Adler's gzip implementation that's used in the GNU version. Other Huffman tables have other (hardcoded) primary table lengths. An even more general Huffman table implementation might look at the number of codes being produced and try to dynamically determine the optimal primary table length; of course, the time spent determining this may very well offset the performance boost of having an optimally-sized table in the first place.
Add a comment:
Completely off-topic or spam comments will be removed at the discretion of the moderator.
You may preserve formatting (e.g. a code sample) by indenting with four spaces preceding the formatted line(s)
And this is crazy
But I've downloaded your whole site
and I've stored it safely :D
Great blog, man

